I found out I had been doing gravity wrong.
This is what I was getting:
There seemed to be gravity, but it was messy.
I had been using the good old (G*m1*m2)/(r^2) equation. However, in an effort to be smart, I calculated the (x2-x1) * (y2-y1) to be the (r^2) value..
WHICH IS TRUE.
And when you apply that force to an object of mass m1, the m1 disappears (F=ma; a=F/m) and you get the acceleration, the pull of gravity.
But, the kicker is, I then have to scale the normal vector out by that. And the normal vector is… just the x component .. is .. (x2-x1)/r.
When you do the whole thing, the acceleration felt is proportional to 1/r^3, not r^2.
So I did that. And I pulled out the gravitational constant, G, to use elsewhere (turns out you can calculate orbital velocities and periods as well).
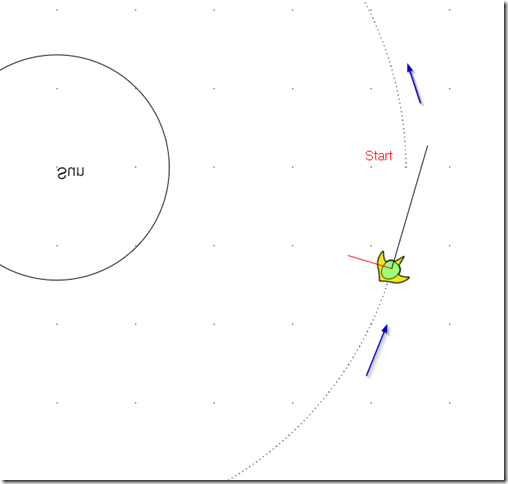
The result:
No matter where you start, no matter your initial velocity and direction (within reason), you get a nice orbit.
What’s more, I could use the maths where “velocity at distance r” can be calculated, as well as “radians per unit time” can be calculated, for a circular orbit.
This means, I could write an autopilot to get you in a circular orbit around a star or planet at a particular distance pretty easily. I think.
However, I also found out that due to gravitational effects of planets, it was very easy to get swept into the sun.. and then gravitationally flung out of the solar system.
So, I changed it when you get within the radius of a planet, gravity is about constant – like it would be at the surface. “Airbrakes”, as it were.
THIS HAS PROMISE! I spent probably an half hour flying around in this simulation, gravity made it so interesting.
it needs one image from the same directory. Otherwise, just run that file.