I shook some dust off some old braincells, and re-remembered some algebra.
My quandry, as hinted by previous post: GIven that I’m 42000 units away from the planet, and I have a max acceleration of 100 units/(sec^2), how much do I accelerate in the direction of the planet?
Some googling finds this: https://van.physics.illinois.edu/qa/listing.php?id=116
d = vt + (1/2)at2
I know my distance, 42000. And I know my a, 100. What I need to calculate is v. But not the one in the equation – that’s starting velocity.
Reverse it. At the planet, starting at v=0, what’s my final velocity when I get to distance d?
The velocity is v = at. So if I can solve for t, then I can plug that in.
d = (1/2) att
tt = 2d/a
t = Math.sqrt(2*d/a)
v = a * Math.sqrt(2*d/a).
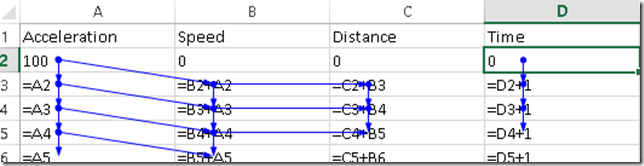
Check the numbers in excel. I set it up like this:
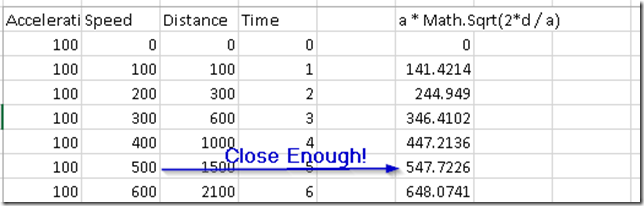
And plug in the formula to see how well it calculates speed:
The drift is due to the coarse 1 second time interval on the calculations, I’m pretty sure.
So, the answer is, if I’m 42000 u away from the planet, and I can thrust at 100 u/s^2, I want to be going 100 * Math.Sqrt(2*42000/100) = 2895 units/sec in the direction of the planet.
- If I’m not going this speed, I need to boost in the direction of the planet.
- If I’m going faster than this speed, I need to boost in the other direction.
To make up for inaccuracies, I’ll set the target velocity to match, say, 90% of my actual available acceleration.
I’m not accounting for my initial velocity at all, even if its not in the right direction. The point is, at any point in space I can caluate what my velocity should be, and what direction it should be in, for the fastest approach to the planet. Whatever I’m doing, change to match that. It should be a nice curve, followed by some nice acceleration, followed by a turnaround, and then some deceleration with some waggles.
Looking forward to implementing it. No time tonight, so I just blogged about my resurrection of Physics 101 instead. Super-excited.